Hydraulic-Electric Analogies: Transmission Comparisons, Part 4

Download this article in PDF format.

The previous descriptions of how ideal machines work were simplifications and are only approximately true. The discussions of hydraulic and electric motors require some re-interpretation because of the effects of adding the losses to the machine models.

For the hydraulic motor connected to a pump, flow from the pump will equal the flow into the motor. However, actual flows are not the same as the displaced (ideal) flow. The ideal equation will yield too high a motor speed because it does not account for internal (volumetric) leakage of the pump and of the motor.

N = 60 Q/D

Where N is the shaft speed in rpm,

Q is the hydraulic flow in volumetric units per second, and

D is the volumetric displacement per revolution.

A similar situation exists with the electrical motor. Recall that electrical power is the product of potential and current (E × I). With armature current, there will be a voltage drop (loss) across the armature resistance. The result is that steady-state speed will be slightly less than would be calculated under ideal conditions.

N = (60/2π) × E/(k_mg × I_F)

where N is the no-load speed in rpm,

E is the applied voltage to the motor input (armature) terminals in V,

K_mg is the motor conversion constant, and

I_F is the field current.

However, more can be gleaned from these ideal equations. Furthermore, some important similarities must be pointed out. The first is that the displacement of the hydraulic motor is perfectly analogous to the field current in the electric motor.

Hydraulicspneumatics Com Sites Hydraulicspneumatics com Files Uploads 2017 01 13 0317 Hp Motion Ctrl F11

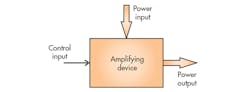
11. Amplifying devices have two inputs, one for power and one for control.

Look at the equations, especially the respective placements for motor displacement and electric motor field current. Both appear in their respective denominators. Which indicates an inverse relationship. With constant flow to the hydraulic motor, increasing the motor’s displacement causes the motor to slow down. The reasoning makes sense: with increased displacement, the motor can turn more slowly yet still absorb all the flow from the pump.

The electric motor has an inverse relationship between the shaft speed and the field current. With constant supply voltage, increasing the field current decreases the motor shaft speed. In other words, the generated counter emf required to meet and equal the fixed power supply voltage can be done at a lower speed due to increased flux, so it slows down in the process.

Controlling the Machines, Transformers, and Amplifiers

Some elaboration is needed regarding machine control via displacement and field current, namely, clarification of what constitutes input. Conceptually, there are two kinds of inputs to any controllable device: power input and control input. Figure 11 provides graphical assistance.

The input to a generator is the mechanical shaft. If the speed increases, the output voltage increases. But we just learned that if the field current is increased, the output voltage increases as well. Is there some significant difference that distinguishes one of those two inputs from the other? The answer is yes, and there are two follow-up questions: First, does the input “know” what is happening at the output? Second, does the power delivered to the output element come through the specific input port? For the input to be the control point, the load changes at the output will not be communicated to the control point. But if the input senses what is happening at the output, then it is a power input point, not a control point.

Hydraulicspneumatics Com Sites Hydraulicspneumatics com Files Uploads 2017 01 13 0317 Hp Motion Ctrl F12

12. Transforming devices, like gearboxes and electrical transformers have no control input port, only input and output ports.

To summarize, the shaft of a hydraulic pump is a power input point because changes at the hydraulic output ports are felt at the input shaft as changes in torque. The more power demanded by the load, the more power has to be delivered through the input shaft. All the power delivered to the load has to enter through the shaft. Similar conditions exist with the hydraulic motor, the electrical generator, and the electrical motor.

Contrast the power input with the control input to the generator. The control input is the field current. It may not be obvious from the discussion so far, but the changes in the output power are not felt at the field input terminals to any significant degree. Analogously, changes in displacement can be made with little effort, even though the pump may be delivering hundreds of kilowatts of output power. The one-way communication from the control point to the output point describes the amplifier principle that is so prevalent in electronics.

In the case of a fixed-displacement pump—say, gear pump—it is not an amplifier, because it doesn’t have a control port, only a power port (Fig. 12). The same is true of, say, an electrical transformer. It has an input power port and output power port, but no control port. And a simple fixed gear ratio is similar. These devices fall into the general category of “power transformers,” or simply “transformers.”.All of the power delivered to the output has to come through the one power input port. There is no control port.

Hydraulicspneumatics Com Sites Hydraulicspneumatics com Files Uploads 2017 01 13 0317 Hp Motion Ctrl F13

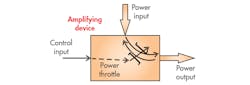
13. An amplifier acts as a power throttle, thus controlling how much power gets delivered to the load, and the two power ports communicate with each other.

Figure 13 shows the amplifying device as a “power throttle” in which the control input throttles the amount of power that is transferred from the power input port to the power output port, and the curved arrows suggest that there is a two-way communication between the power input and power output, but there is no link from the output to the control input. That’s a one-way street. The amplifier is very much like a valve, and in fact, hydraulic valves are terrific amplifiers, especially servo and proportional valves.

It is an interesting exercise to ponder machines and evaluate whether or not they are amplifiers or transformers. Consider the internal combustion engine. It is an amplifier of gargantuan performance specifications. The power output point is the crankshaft, the power input point is the carburetor or fuel injectors that deliver the input power, and the control input is the throttle and injector control. It’s gratifying indeed to know that when driving to work in the morning, the output power needed to propel the vehicle does not have to go through your throttle foot. On the other hand, consider riding to work on a bicycle.