Designing closed-loop circuits for stability

Fluid power system designers are becoming increasingly involved in electrohydraulic closed-loop control-system applications. Many have told me that control-loop instability at system start-up is one of the problems they encounter most frequently. Trial-and-error attempts to correct these problems are time-consuming and expensive. More often than not, it is necessary to seek help from someone with more experience in feedback-control principles to come up with a solution acceptable to the customer. In some cases, designers have a mental block about hydraulics and turn to electrics as a perceived better way to solve their control problems.

I’ve seen this happen over and over again during my 40-year career in the electrohydraulic control field. Usually the problem occurs because the control-loop components were selected on the basis of their steady-state characteristics — without an understanding of their dynamic characteristics and how they influence control-loop stability. Much of the textbook material dealing with control-loop stability and attainable closed-loop performance is based on sophisticated mathematical treatment of the subject. Many servo system seminars use the same approach, which generally goes right over the heads of most fluid power system designers.

I believe that designers need a simpler way to understand control-loop dynamic behavior, one that can be used to size and select control components so as to ensure stability. Such an approach could predict control-loop performance before committing the project to hardware. This could greatly enhance users’ perceptions of the designer’s ability to provide hydraulic solutions to control problems, particularly when electronics loom as the alternative solution.

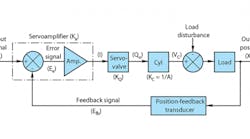
I use an experience-based approach to dynamic analysis of servo-loops that reduces a loop’s dynamic characteristics to several simple equations. These equations can be solved to establish servo-loop stability and find the allowable loop gain that a stable closed loop can tolerate. Then the loop gain can be used to approximate closed-loop servo performance characteristics. To walk through this approach, consider the most common type of electrohydraulic linear-position servo as diagrammed below. The basic working sequence of this position servo is:

1. Input signal E_c commands output position X_o.
2. Actual output X_o is measured and fed back as position feedback signal E_fb.
3. Input E_c and output E_fb are compared to produce error signal E_e.
4. Amplified error signal is servovalve input I and produces cylinder velocity V_c.
5. Cylinder drives toward commanded position X_o and attains it when error signal E_e is zero.
6. Feedback measures load disturbance change.
7. Error signal E_e produces servovalve input I to force output to return to commanded position X_o

Servo-position gain X_o / E_c is equivalent to the reciprocal of position-feedback transducer gain l / K_fb. Therefore, rated input signal E_c will be determined by the feedback transducer gain multiplied by the rated cylinder or stroke. Thus, selection of the feedback transducer will determine the servo’s rated input signal.

The servovalve and cylinder must be sized to meet the application’s load-driving requirements in terms of cylinder stroke, maximum velocity, and force. The servoamplifier will be selected for compatibility with the requirements of the command and feedback signals plus servovalve drive-signal requirements. It also will have adjustable gain Ka, with a range to meet allowable servo-loop gain requirements.

The loop-gain constant

Servo-loop gain is the product of all the gains in the servo loop with feedback path open-feedback signal (E_fb) not connected to the servoamplifier. This gain is expressed as:

K_v = (K_Q×K_a×K_fb) / A                   (Equation 1)

where:
K_v is loop-gain constant, sec–1
K_a is servoamplifier gain, mA/V
K_fb is feedback-transducer gain, V/in.
K_Q is servovalve-flow gain, (in.³/sec)/mA, and
A = cylinder net effective area, in.²

The control-component gains in Equation 1 are usually the steady-state or zero-frequency gains. The significance of the loop-gain constant (sometimes called the loop-velocity constant)  is that it is a measure of the cylinder velocity generated to correct a position error. For example, the cylinder velocity generated by a position error would be:

V_c = E_e×K_v / K_fb                               (Equation 2)

where:
V_c is cylinder velocity, in./sec, and
E_e is error signal.

The greater the cylinder velocity generated by an error signal, the faster the servo-loop response is to correct that position error. It then follows that the faster the position error is reduced to zero, the greater the control accuracy of the servo loop. To attain a highly accurate servo loop, it becomes evident that K_v should be as high as possible.

You might think that after selecting the servovalve, cylinder, and feedback transducer to meet the application load-drive requirements, the servoamplifier gain should be adjusted to the highest possible level for high servo-loop accuracy. This strategy is highly flawed, because it gives no consideration to the dynamic behavior of the control components when the control loop is closed. It usually results in problems with servo-loop stability, unless the loop-gain constant is quite low. But a low loop-gain constant reduces accuracy.

Control-loop dynamics

To determine the highest K_v that the servo loop can tolerate with acceptable stability, one must understand the control component’s dynamic characteristics and how they interact to influence control loop dynamic behavior. To describe these control-component dynamics and their interactions in the control loop, we could use an esoteric mathematical approach involving transfer functions based on state-variable and classical Laplace representations. Or we could use a variety of frequency-response graphs or Bode plots to illustrate and explain control loop dynamic behavior. However, these approaches would be virtually meaningless to anyone without an extensive background in higher mathematics. Instead, we'll cover discuss control-loop dynamics in everyday language.

Control loop response to a constant-amplitude, sinusoidal input signal of increasing frequency, with the feedback path open or open-loop, provides a convenient approach to analyzing its dynamic behavior. This type of response describes the changes in loop gain and phase lag produced by the control component dynamics as the input signal is increased from a reference frequency to the highest frequency of interest. It will show the relationships between loop gain and phase lag at specific frequencies used to establish the relative stability of the control loop when the loop is closed (when the feedback signal is connected to the servoamplifier).

The dynamics of the diagrammed basic position servo can be treated as consisting of a dominant damped resonance and an integration, accompanied by a loop-gain term. The cylinder dynamics of interest consist of an integration and a damped resonance. The servovalve dynamics of interest consist of a damped resonance. The loop-gain term is K_v from Equation 1. The dominant damped resonance is the resonance in the control loop, which exerts a controlling influence on the control loop’s dynamic behavior over the frequency range of interest. It will exhibit the lowest resonant frequency of all resonances present in the control loop.

A damped resonance exhibits dynamic behavior similar to a simple spring-mass system that is excited by a constant-amplitude forcing function of increasing frequency. It exhibits a relatively constant vibratory amplitude until the frequency begins to approach the resonant frequency. Nearing the resonant frequency, the vibratory amplitude increases and peaks at or very near the resonant frequency. As the forcing frequency increases beyond the resonant frequency, the vibratory amplitude shrinks rapidly. The vibratory amplitude’s peak is a function of the damping factor. Small (0.30 or less) damping factors produce large peaks; larger (0.50 or greater) damping factors produce modest or no amplitude peaks.  As frequency increases, the rate of change of the phase shift between the vibratory amplitude and the forcing-function amplitude is influenced by the damping factor. However, all resonances, whether lightly or heavily damped, exhibit a 90° phase lag at the resonant frequency. The amplitude peak at or near the resonant frequency and the 90° phase lag at the resonant frequency are key dynamic characteristics of the damped resonance. They significantly influence closed-loop stability. To reiterate, the dominant damped resonance is the resonance with the lowest resonant frequency. It is also necessary to know whether the dominant damped resonance is lightly or heavily damped, because an amplitude peak exerts a significant influence on closed-loop stability criteria.

The input flow rate to the cylinder generates a cylinder velocity. Cylinder output, as indicated by the feedback signal, is displacement or position. Because the indicated cylinder position over any time interval is the product of cylinder velocity and the time interval, cylinder position is the time integral of cylinder velocity. Hence, the term integration is used. The dynamics of integration act on the loop gain to attenuate it at a constant rate of 20 dB/decade (a 10:1 gain decrease for each 10:1 frequency increase) as the input frequency increases. The dynamics of the integration also contribute a constant 90° phase lag to the control loop.

You should see from this discussion of control-loop dynamics that the dynamics of the integration and dominant damped resonance act on the loop gain to attenuate it at a constant rate until the loop gain is amplified by the resonant peak of the dominant damped resonance, after which it attenuates again rapidly. With respect to phase lag, the 90° phase lag produced by the integration combines with the 90° phase lag of the dominant damped resonance at its resonant frequency to produce a control loop phase lag of 180° at the resonant frequency. This frequency is sometimes called the phase crossover frequency, and is an important factor for determining control loop stability criteria. Another important frequency is that when the loop gain has attenuated to unity (1.0 sec^-1). This frequency is often called the gain crossover frequency.

Dominant damped resonance

Before further discussion about control-loop stability criteria, we should establish a method to determine dominant damped resonance in numerical terms. For our purposes, the cylinder and the servovalve are the control components that produce resonance. Thus, we need to establish the resonant frequencies of these two control components. The resonant frequency of the cylinder is given by the expression:

W_r = (4BA²/VM)^1⁄2                             (Equation 3)

where:
W_r is cylinder resonant frequency, rad/sec.
B is fluid bulk modulus, psi
V is total fluid volume trapped between the piston and servovalve output ports, in.³ , and
M is load (including piston and rod) mass reflected to the cylinder, lb-sec²/in.

When single-rod cylinders are used, the annular piston area will result in a conservative value for the resonant frequency. A conservative value for the fluid bulk modulus would be 150,000 psi. Cylinder resonances are normally lightly damped (i.e. a damping factor of 0.30 or less) and will exhibit significant amplitude peaks. Also note from Equation 3 that, to attain the highest possible cylinder resonant frequency for a fixed-mass load and specific hydraulic fluid, the ratio A²÷V should be maximized.

For servovalve resonance, take the resonant frequency as the frequency when the servovalve exhibits a 90° phase lag. Normally, servovalve resonance is heavily damped (i.e. a damping factor of 0.50 or greater) and will exhibit little or no amplitude peak. The servovalve resonant frequency and amplitude peak condition can be readily determined from frequency-response plots provided by the valve manufacturer.

Compare the resonant frequency of the cylinder with the servovalve resonant frequency. The lowest resonant frequency will determine the dominant damped resonance. The comparison also will reveal whether the dominant damped resonance is lightly or heavily damped. The damping of the dominant damped resonance is extremely important when establishing criteria for  closed-loop stability.

Degrees of stability

Stability is probably the most important characteristic of a closed loop. It refers to the ability of the closed loop to respond to an input command and attain the commanded output without sustained oscillation. There are relative degrees of closed-loop stability. For example, the output could rapidly rise to the commanded output, but overshoot by a significant amount and then have a number of undershoots and overshoots before settling at the commanded output. This condition still could be considered as one with a minimum degree of stability, because the output eventually does settle at the commanded output.

A second example of stability would be where the output rises at a slower rate toward the commanded output, then settles at the commanded output after a small overshoot and undershoot. A third example of stability would be where the output rises at a relative slow rate to the commanded output with no overshoots or undershoots.

Because the response time of interest is the interval between application of the input command and attainment of the steady-state commanded output, each of these examples could have a significantly different response time. In the first, the response time might be relatively long due to the long settling time imposed by numerous overshoots and undershoots. In the second example, the response time might be relatively short due to the minimum settling time imposed by small overshoots and undershoots. In the third example, the response time could be even longer than that in the first example due to the slow rise toward the commanded output even with no overshoots and undershoots.

Although the first example could be considered as having a minimum degree of closed-loop stability, the other examples could be considered as having a higher degrees of closed-loop stability. From a practical standpoint, the second example could be considered most desirable, because the closed loop is highly stable and the response is a good compromise between rise time and settling time. This type of output response could be designated as well damped.

The degree of stability of any closed-loop servo is determined by the open control-loop relationships between the loop gain and phase lag at the phase crossover frequency (i.e. the frequency at which the loop phase lag is 180°) and the gain cross-over frequency (i.e. the frequency at which the loop gain is unity). These relationships are called the gain margin and the phase margin.

Gain and phase margins

The gain margin is defined as the ratio of unity (1.0) to the loop gain at the phase crossover frequency. For a highly stable closed loop with a well-damped output response, the gain margin should not be less than 2.5. This means that the loop gain at the phase crossover frequency should not exceed 0.40 sec^–1. Gain margins significantly greater than 2.5 can result in closed-loop output responses that are heavily over-damped. Gain margins ranging from 2.5 to 3.0 are good design targets.

The phase margin is defined as the difference between 180° and the loop phase lag at the gain crossover frequency. For a highly stable closed loop with a well-damped output response, the phase margin should not be less than 45°. This means that the loop phase lag at the gain crossover frequency should not exceed 135°. Phase margins considerably greater than 45° also can result in a heavily over-damped closed-loop output response. A phase margin between 45° to 60° is a good design target.

Note that although both gain-margin and phase-margin criteria for a stable closed loop must be satisfied, there are specific situations where either the gain-margin criteria or phase-margin criteria will be dominant in establishing the degree of closed-loop stability. When the dominant damped resonance in the control loop is lightly damped, the gain-margin criteria dominate, because of the gain-amplification peak at the resonant frequency introduced by the lightly damped resonance. In such a case, establishing the gain margin to ensure a well-damped closed-loop response will automatically result in an adequate phase margin.

When the dominant damped resonance is heavily damped, the absence of a gain-amplification peak at the resonant frequency allows the phase-margin criteria to be dominant. If this is the case, establishing the phase margin to ensure a well-damped closed-loop response will automatically result in an adequate gain margin.

Before continuing on to the simple equation used to approximate closed-loop servo performance, we should summarize the key points of the preceding discussions as they provide the basis for using the simple equations. Those points are:
• the allowable K_v is controlled by the control-loop stability criteria. It is a measure of the cylinder velocity generated to correct a position error. The greater the loop-gain constant, the greater the steady-state and dynamic accuracy of the closed-loop servo
• closed-loop relative stability is defined by the gain margin and the phase margin. The gain margin is established at the phase cross-over frequency and the phase margin is established at the gain cross-over frequency, and
• the phase cross-over frequency is equivalent to the resonant frequency of the dominant damped resonance. The gain crossover frequency will be determined by the phase lag versus frequency characteristics of the dominant damped resonance in the frequency range below the resonant frequency.

Performance-approximation equations

The simple equations that can be used to approximate closed-loop servo performance assume that the basic position servo is an uncompensated servo loop. This means that the servoamplifier contains no frequency-sensitive electronic networks to compensate for control-component dynamics that could significantly limit the allowable loop-gain constant for a stable closed-loop. (Discussion of servo loop compensation is far beyond the scope of this text and therefore is omitted.)

When the dominant damped resonance is a lightly damped cylinder resonance, the gain margin will control the relative stability of the closed loop. For this case, the allowable loop-gain constant can be approximated from the equation:

Kv = 2δ_rW_r / g                                       (4)

where:
δ_r is resonance damping factor (0.4 or less), dimensionless, and
g is gain margin (2.5 or greater), dimensionless.

Because the true damping factor of the lightly damped resonance is rarely known, experience indicates that 0.20 is reasonable estimate for servovalve-controlled cylinders. Assuming a gain margin of 2.5 and a damping factor of 0.20, Equation 4 reduces to: 

Kv = 0.16 ✕ W_r                                       (5)

When the gain margin is used to establish relative stability of a closed loop containing a lightly damped dominant resonance, a satisfactory phase margin is automatically established at the gain cross-over frequency. Assume that the loop-gain constant approximated from Equation 4 or 5 was referenced to a frequency of 1.0 rad/sec. Then the 20 dB/decade gain attenuation rate introduced by the integration dynamics allows the gain cross-over frequency to be approximated from the loop-gain constant. For this case, it can be shown that loop gain constant K_v in sec–1 units is equivalent to gain crossover frequency W_g in rad/sec units. Thus:

Kv = W_gc                               (6)

The gain crossover frequency is important because it defines the boundary between closed-loop control action and open-loop control action. Feedback control is only effective when the loop gain is greater than unity. Therefore, the closed-loop control action of a closed-loop servo — responding to dynamic input signals — is limited to the frequency range below the gain crossover frequency. Above this frequency closed-loop control is no better than open-loop control.

When the dominant damped resonance is a heavily damped servovalve resonance, the absence of an amplification peak in its output response permits the phase margin to control the relative stability of the closed loop. Using the phase margin to establish closed-loop stability will automatically establish a satisfactory gain margin. Remember, the phase margin is established at the gain crossover frequency and must be at least 45°. For a 45° phase margin, the loop phase lag at the gain crossover frequency would be 135°. Because the integration dynamics contributes a constant 90° phase lag, the servovalve contributes the balance of the loop phase. Therefore the gain crossover frequency would be the frequency when the servovalve exhibits a 45° phase lag.

Having established the gain crossover frequency, we can use the 20 dB/decade gain-attenuation rate, introduced by the integration dynamics, to approximate K_v from the gain-cross over frequency. This approximation is the same as that shown in Equation 6.

Simple methods have been presented to approximate the loop gain constants and gain cross-over frequencies for control loops containing either a lightly  or heavily damped dominant resonance. Key points to remember: the loop-gain constant will limit closed-loop servo steady-state accuracy and the gain cross-over frequency will limit the frequency range over which feedback control action is effective.

General guidelines

Because fluid power designers may have little prior knowledge of allowable loop-gain constants associated with various application areas, here are some general guidelines based on experience. For servo loops with feedback-control action exceeding that of common regulators, the loop gain constant should be greater than 5.0 sec^–1. The loop gain constant for mobile equipment applications will range from 8.0 to 12.0 sec^–1; general industrial applications from 20 to 30 sec^–1; motion simulators from 25 to 70 sec^–1; machine tools, fatigue testing equipment, tensile testing equipment from 100 to 500 sec^–1. It also is likely that control-loop compensation will be necessary to attain desired loop-gain constants for some applications. However, the loop-gain constant approximation for an uncompensated control loop can point up the need for control loop compensation.

The loop-gain constant and gain crossover frequency can be used to approximate position control-loop performance parameters, such as positioning error, following error, and dynamic-response capability.

Performance parameters

Positioning error is the difference between actual steady-state output position and commanded output position. Steady-state output position is attained when cylinder velocity is zero. However, servovalve and cylinder anomalies can be present which require an error signal to exist in order to attain zero cylinder velocity. Servovalve anomalies include hysteresis, threshold, pressure null shift, and temperature null shift. Cylinder anomalies include break-out friction, piston-seal leakage, and motion lost at the mounting connection. For a well-designed servocylinder and a typical industrial-grade servovalve, a servovalve input signal of about 6% of rated signal current is usually enough to accommodate these anomalies. Because response to an output position change, due to an input command or load disturbance, is a function of the cylinder velocity generated to correct the error, the positioning error or uncertainty due to control component anomalies can be expressed as:

Xe = 0.06 Vc / Kv                          (7)

where:
Xe is positioning error, in.

The error approximation from Equation 7 would be a maximum if all anomalies were present simultaneously.

Following error is of interest when the position servo must follow motion-control profiles consisting of ramps and holds. It is the difference between actual output position and commanded output position, when the servo is subjected to a ramp command input. The slope of the ramp command represents a steady-state cylinder velocity. Therefore, an error signal must exist to produce the cylinder velocity. This position error is the following error and can be approximated by the expression:

X_f = V_c/ K_v                            (8)

where:
X_f is following error, in.

The time lag between the actual output position and the commanded output position can be approximated by dividing following error Xf by cylinder velocity Vc. Equation 8 shows the time lag is equivalent to the reciprocal of the loop gain constant, i.e. 1/ K_v.

Servo response to time-variant inputs is of interest when the servo is used in applications where rapid changes in input signals and randomly occurring load disturbances are prevalent. Servo response, in terms of dynamic-response bandwidth, is usually specified as the frequency when servo output has attenuated to 0.707 of the reference frequency output. This is commonly called the –3 dB frequency. Because the gain cross-over frequency defines the frequency limit for feedback-control action, it can be used to approximate the dynamic-response bandwidth. Experience shows that neglected non-linearities in the control loop can cause the –3 dB frequency to extend somewhat beyond the gain cross-over frequency. Therefore, an experience-based approximation of dynamic-response bandwidth would be:

BW = 1.2 × W_gc                                 (9)

where:
BW is –3 dB bandwidth, rad/sec, and
W_gc is gain cross-over frequency, rad/sec.

Although the actual closed-loop position servo contains higher order dynamics than those included in this simplified dynamic-analysis process, its output response over the frequency range up to the gain cross-over frequency is similar to that of first-order lag function. Therefore, we can approximate its-step input response by a simple time-constant equivalent to the reciprocal of the loop-gain constant:

T = 1 × K_v                                                                 (10)

where:
T is time to reach 63% of commanded output, sec.

When K_v has been established, using control-loop stability criteria for a well-damped closed-loop output response, the time to reach 90% of commanded output would be equivalent to about 3 time constants or 3T.

A useful tool

In conclusion, we can state that the simple dynamic analysis process offers the hydraulics practitioner a useful tool to approximate servo-loop performance limits, based on the preliminary selection of control components to be used in the servo loop. These results can be compared with the customer’s specifications to determine any variances. If variances are observed, it may be necessary to compensate the servo loop (electronic compensation in either the servo-loop forward path or feedback path), select different control components, or change the load-driving structural — or question the validity of some of the customer’s specifications.

For example, suppose the dominant damped resonance was produced by the cylinder/load combination and had a resonant frequency of 10 Hz (62.83 rad/sec); and that the customer specified a 20-Hz (125.67 rad/sec) servo bandwidth. The simple dynamic analysis shows that the servo loop was incapable of a 20-Hz bandwidth. In such a situation, a practical means for increasing the resonant frequency of the cylinder/load combination to an acceptable value would have to be found. Or instead, the need for a 20-Hz servo bandwidth could be called to question.

Another situation commonly occurs when the customer’s specification calls for a very high level of positioning accuracy. Simple dynamic analysis results for the uncompensated servo loop may show that the allowable loop-gain constant for a stable servo loop is insufficient to meet this positioning accuracy. In this case, it may be possible to use electronic compensation to increase the loop-gain constant to an acceptable level. On the other hand, the customer’s positioning accuracy specification may be too stringent.

In cases where the designer offers the customer a packaged servo system (servocylinder with integral feedback transducer, servovalve, and companion electronic controller), the positioning-accuracy and servo-bandwidth claims of the packaged system’s manufacturer usually are presented on a no-load basis. In actual practice with the servo driving a load, positioning accuracy and servo bandwidth will vary significantly from the no-load specifications. Simple dynamic analysis can predict these variances so that neither the customer nor the designer will be surprised when such a system is put into service.

One final point: the results given by the simple dynamic-analysis process apply equally to servo loops using analog or digital electronics. When electronic compensation of the servo loop is necessary to improve servo-loop performance limits, analog servocontrollers use hard-wired compensation networks, while digital servocontrollers use programmable digital signal processors. In either case, the electronic compensation must be in compliance with the stability criteria necessary to obtain a stable closed loop.

Hydraulic designers must remember that servo performance limits will be dictated primarily by the selection of the hydraulic control components to be used in the servo loop. Electronics cannot compensate for the shortcomings of hydraulic components. The simple dynamic-analysis process can help to avoid such situations.