This article was originally published in the October 1948 issue of Applied Hydraulics magazine. It was written by E.H. Buller and B. H. Ford, who were project engineers at the Equipment Laboratory, Engineering Division, AMC, Wright Patterson Air Force Base, Dayton, Ohio.
The recognition of the guided missile as a realistic military weapon has opened another field for the application of fluid flow principles. In commercial aircraft design, hydraulics has long been an established workhorse; its power operates landing flaps, landing gear, shock struts, brakes, propeller pitch controls, turret drives, autopilots, servos, and similar assemblies.
The German V -2 type missile in an early stage of launching flight at White Sands, New Mexico. (All photographs courtesy of the United States Air Force)
The new fields of supersonic aircraft and guided missile flight will, undoubtedly, put further demands on the hydraulics industry to deliver hitherto unprecedented performance to satisfy new design and operating requirements.
For the purpose of clarification, a guided missile differs from the normal concept of conventional aircraft in that it is essentially a flying body stabilized in altitude, which can be guided through space, either by remote control or by means of self-contained guidance equipment, to a specified target. Another difference is that once a missile is fired or launched, it is, except through radio links, beyond manual operation or manipulation of integral equipment. Accordingly, if the mission is to succeed to any degree, equipment must function properly and dependably.
It is evident from the above considerations that design criteria imposed upon missile equipment will tax the designer's ingenuity m1d judgment. A further complication arises from the expendable nature of this equipment- the missile in part or whole is a one-shot affair. In this respect, the designer will also be asked to simplify design and production details to the highest practical degree and to achieve an optimum economy without sacrificing dependability of performance.
German Guided Missile Developments
The cessation of hostilities and subsequent removal of security barrier revealed the comparatively startling advances made by German scientists and designers in the missile field. A multitude of both subsonic and supersonic craft of varied types was either under development or developed for operational use; some of these missiles had reached a high degree of performance. Notable among the latter were the popularized V-1 and V-2 type. In some respects, the V-2 typifies a successful craft and is a standard research vehicle currently used both in this country and abroad.
The wartime V -2 was a ground-launched, self-propelled bomb, 45 feet high and carried a 2,000-lb warhead. A typical fuel load consisted of 7,000 lb of alcohol and 11,000 lb of liquid oxygen, bringing the total weight of the fueled missile to 28,000 lb. Complete burning time was limited to approximately 60 seconds. After fuel cut-off, the missile became a free body and assumed the usual trajectory of a projectile. The maximum velocity, which occurred at the time of thrust cut-off, was approximately 3,800 miles per hour.
It is quite apparent that the fuel consumption and power required to drive pumping machinery are beyond normal expectations. Moreover, the fuel was fed into the burners by two pumps, both steam turbine driven. The steam was generated on demand by the decomposition of approximately 300 lb of highly concentrated hydrogen peroxide. Products of this decomposition were superheated steam at 700° F and 700 psi and some free oxygen. The total weight of pumps and turbine was·220 lb.
The control surfaces of the missile were operated by means of individual hydraulic servos. System pressure was developed by electrically-driven gear pumps totally submerged in the oil sump to prevent formation of air pockets and to reduce line length to an absolute minimum. The latter requirement was imposed by the installation of the pump and servo units directly into the tail fins. It should be remembered that space limitations in most missiles are almost always critical, regardless of the equipment concerned.
Typical lineup of hydraulic components of a control system pump, accumulator, control valve with electric input, and servo with electric displacement follow-up.
Applications of Hydraulics
Contemporary missile designs account for various applications of hydraulic equipment, basically to deliver fuel and to operate control surfaces. Liquids to be pumped might include oil, alcohol, liquid oxygen, hydrogen peroxide and various other fuels and oxidizers. Hydraulically operated servos might require system pressures ranging from a few hundred to beyond 5,000 psi, whereas fuel delivery systems might be measured in terms of V-2 flow requirements.
It seems reasonable to expect tailor-made equipment developments for prototype missile applications, but standardized systems and components are the necessary aim of the Services and missile producers. Ground handling and launching equipment for missiles also utilize hydraulic principles for their operation.
Control Systems
Hydraulically operated servomechanisms have been a highly respected standard in industry for many years. The principle has also been applied with repeated success to the design of aircraft and missile autopilots, or control systems, as they are referred to in the missile vernacular.
The control system is of special interest inasmuch as hydraulics is competing with electrical, mechanical and pneumatic systems in the field of missile control equipment. Allowances in performance of such systems are progressively being diminished to finite values. Time constants are now being expressed in terms of hundredths and thousandths of a second, which does not allow much margin for error. Serious competition between the various methods of operation for the greatest measure of performance has begun.
In an attempt to give a rounded picture of the problem confronting the designer of such control systems, the following paragraphs are devoted to a concise discussion of the elementary theory and evaluation factors of a guided missile system.
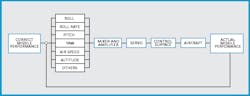
The control system of a guided missile is synthesized as a closed loop system, i.e., if an error occurs in the missile's position, velocity, acceleration, air speed, ground speed, altitude or any other parameter of its flight, this error is detected and measured by some type of indicator which in turn actuates the servomechanism a n d subsequently attempts to reduce the error to zero. Such a closed-loop system is shown schematically in the illustration.
Schematic diagram of a guided missile control system.
To better understand the many and varied aspects involved in controlling a guided missile or pilotless aircraft in general, visualize the problem of designing a control system for some guided missile in particular. First, the exact actions desired of the craft must be determined. Specifications regarding the mission of the missile are decreed by tactical purposes, but the designer must have a thorough understanding of the mission to create an ultimate performance toward the achievement of each type of mission. Sometimes the task of the control system designer is difficult, and the work of the propulsion engineer is comparatively easy; again, the opposite is true.
The craft may be designed to be especially adaptable to any of the following missions:
(1) Launch from ground and pursue long-range course to a selected type target on the ground
(2) Launch from the ground and pursue a collision course to a target in the air
( 3) Launch from the air and pursue a collision course to a target in the air
(4) Launch from -the air and pursue a short-range course to a selected type target on the ground
(5) Launch from the ground and pursue a short-range course to a target on the ground, or
(6) Launch from the ground and respond to radio control.
Depending upon the immediate purpose of the craft, any of the following maneuvers or combinations of maneuvers may be desired:
(1) Straight and level flight
(2) Straight and level flight at a given altitude
(3) Straight and level flight at a desired altitude and air speed
(4) Take-off, followed by straight and level flight
(5) Take-off, straight and level flight, coordinated banks and turns
(6) Take-off, flight on a predetermined course, descent by parachute
(7) Take-off, subsequent flight by radio beam
(8) After release from another aircraft, follow a collision course to a designated object, or
(9) Take-off, respond to the controls of an operator on the ground.
Creating a control system that will accomplish any combination of the above type of maneuvers involves a complicated array of controls. Presume that the missile has just been released by an aircraft and is in the atmosphere traveling at the desired speed, headed in the desired direction, possessing power to maintain selected airspeed and experiencing no immediate disturbance. Should an error occur in the direction, for example, because of a gust of wind or another factor, there are two methods of giving a missile a push to the desired direction:
(1) Moving an aerodynamic control surface and creating a force or torque by means of the air through which the vehicle is moving, or
(2) Activating a lateral jet, an explosion or a similar inertial reactor.
If the missile is designed to fly through the stratosphere, where the air becomes progressively thinner, the latter type of control is a necessity. Otherwise, because of the fuel involved and other practical considerations, the aerodynamic control surface affords the easiest solution. If aerodynamic means of control are chosen, there are several methods by which the control surface may be moved relative to the error. One method provides movement of the surface at a constant velocity above a certain level.
Systems of this nature are often referred to as "bang-bang" control. In some instances, the control surfaces are self-streamlining after the error reaches a zero position; such a condition removes the necessity of the servo motor cranking the surface to a neutral position after the missile has responded to the control.
Another method, known as a "proportional torque" system, applies a torque to the control surface proportional to the error that exists. As in the previous case, the surfaces are usually self-streamlining. This method has the advantage of the desirable tendency to provide for constant reaction of the missile to the control surface.
For instance, when the vehicle reaches atmospheres where the effect of the control surface is reduced, the same torque will move the control surface farther out into the airstream and thus tend to maintain the same amount of control. Yet another type of system has provisions for moving the control surface angularly into the airstream at an angle proportional to the error. This is known as a "proportional control" system.
Proportional Control System
There are other types of systems, but for this discussion assume that proportional control would be used for the stabilization of a missile. A simple pendulum illustrates a proportional control system. By definition, a servomechanism must be characterized by an amplification of power. A pendulum does not have this characteristic, but it nevertheless has the same dynamic performance.
To further illustrate this condition, recall that an aerodynamic control surface will create a torque that is nearly proportional to the angle at which the surface is extended into the air stream, particularly for the small angles over which a control surface normally operates. It follows, then, that a proportional control system will provide a restoring torque to any axis of a missile that is proportional to the angular error that exists about the axis. Similarly, a pendulum has a restoring force relative to the vertical position that is proportional to the angular· error from the vertical position. If a pendulum is given an unbalancing disturbance, it would tend to oscillate.
A missile with this type of control given an unbalancing disturbance would also tend to oscillate. This is an undesirable characteristic and steps must be taken to eliminate such a reaction. The oscillations in a pendulum can be damped out by placing the pendulum in a fluid more viscous than air. Damping is defined as an opposing force or torque which is proportional to the velocity of an object.
There are two general methods by which the oscillations in a missile can be damped out:
(1) Aerodynamic damping, which is a result of the air tending to prohibit rotation about any axis, or
(2) Prediction circuit damping.
In the first method, the aerodynamic damping on the missile is a fixed quantity that cannot be governed by the control system designer. Because of the small wings or fins of the typical missile, the worth of this type of damping is usually small but it has some value.
Prediction circuits measure the rate of roll of the missile about any axis and reduce the proportional control by an amount relative to the rate of rotation about that axis. Reducing the proportional control has the same effect as adding an opposing torque, which is relative to the rate of rotation and thus damps out oscillations. Prediction circuits can easily provide excessive damping to the extent of causing immovability in a missile. This condition is similar to a pendulum trying to oscillate in an atmosphere of mud. To reduce an error quickly to zero and prevent overshooting and cause oscillations, it is better to provide critical damping or slightly less. FIG 4
Control System Considerations
It is obvious that a control system is not basically complicated, but there are several factors which may greatly upset the simple equations that would otherwise apply for such a system.
To list a few:
(1) A time lag always exists between a signal and the response to the signal.
(2) Various ratios are not actually proportional.
(3) Mechanical movements and electrical quantities are limited.
(4) Weight, size and shape of units are restricted.
(5) System components will frequently become unworkable at climatic extremes.
(6) The maximum power available is often limited.
Because a proportional control system can be represented by a simple spring and mass associated with a certain amount of viscous damping, it is evident that inertia, spring constant and coefficient of damping become primary terms in the equations which pertain to the system. Inertia, aerodynamic coefficients and similar parameters must be considered in the equations pertinent to any guided missile In a simple spring and mass system, the "natural undamped frequency" of such a system is a common term. This natural frequency is given by the equation:
Wn = (k/M)1/2
where k is the spring constant, and
M is the mass.
Similarly, the natural frequency of a missile having proportional control is comparable. This natural frequency is given by:
Wn = (c/I)1/2
where c is the effectiveness of the control surface about the axis under consideration, and
I is the moment of inertia about that axis.
Typical units of c would be pound-feet per radian. Because of the damping and other considerations, the missile might not actually oscillate at this frequency.
Time Lags
Time lags that occur in the controlling servo are the primary reason for complications in such· equations; time lag exists in every circuit and movement. For example, if an electrical voltage is generated that indicates an error in the direction of flight, the voltage must be relayed to an amplifier.
Because of inductances in the circuit, the amplifier receives the signal a few thousandths of a second after the error occurred. The amplifier takes upward of a few microseconds to amplify this signal. A few thousandths of a second later this voltage will operate a small control device. After another few thousandths second the main power unit will start to operate. In another fraction of a second the control surface will finally begin to move. However, this movement occurs only after a time lag ranging from a few hundredths of a second to a more substantial time gap after the original error signal was initiated.
In the meantime, the error may have increased considerably. It is clear that any control mechanism which cannot move the control surface before the missile can respond appreciably to an assumed error in the position of the surface cannot be expected to exert control. If a one- or two-degree deflection inadvertently remains in the control surface, some missiles can turn completely over in a few hundredths of a second. It is evident that the time lag problems in servos can assume large proportions.
The Size Factor in Control Design
The time required for a missile to respond to a movement of a control surface is directly a function of the mass of a missile and inversely a function of the effectiveness of the control surfaces. As a missile becomes smaller in size, the problems of building an automatic control become increasingly more difficult. Working space is at an absolute premium.
For example, one requirement could demand the building of a complete electronic circuit containing upwards of fifty tubes in a space of less than 75 cubic inches. At supersonic speeds, it requires relatively large forces and torques to move a control surface into the airstream. Considerable research and a high order of skill are necessary to design a unit sufficiently powerful to move a control surface in a fraction of a second and small enough to require only a few cubic inches of space.
Error Detection Essential
All control systems and related servomechanisms rely upon the detection of an error to operate in the proper manner. In guided missile work, finding the error is in itself a difficult task. For instance, the basic problem of discovering or creating a device that will accurately indicate a direction for any length of time is not as easy as it may appear. A magnetic compass is
rendered useless by the caliber of accelerations present in the flight of a missile, and a gyro compass drifts off course in a short time.
It is often necessary for navigation and general stabilization to know the true vertical from the earth at all times; it is difficult to build a precise, vertical indicator. Frequently too, instruments that perform well in the laboratory cannot tolerate the vibration and acceleration of a missile in flight and certainly will not survive the shock of launching.
The Computing Circuit Problem
Extensive computing circuits are often incorporated into the control systems of guided missiles. Such circuits are called upon to add, multiply, integrate and perform numerous other calculations for guidance purposes. It would be highly desirable to create a control system which would cause the missile to perform in the desired manner without reference to any exterior influence. Such a system is referred to as a "inertial reference" system. It is possible to detect the following quantities without reference to external influences and without knowledge of position with respect to the earth:
(1) Direction and value of linear acceleration
(2) Direction and value of angular acceleration, and
(3) Direction and value of angular rotation.
It is not possible to have direct detection of the following quantities:
(1) Direction and value of linear velocity, and
(2) Linear position.
An inertial reference system must, among other things, integrate linear acceleration once to obtain linear velocity and twice to obtain linear position. Such circuits would be called upon to integrate with utmost accuracy and integrate over long periods of time. Design of such devices progresses slowly and involves a considerable effort, time and cost. The foregoing is representative of but one of the many problems in the design of computing circuits.
A V-2 missile being raised to its vertical launching position by a twin-cylinder hydraulic lift.
Hydraulic Controls
Hydraulic mechanisms have won a place in many applications associated with missile work. Fluid affords a means of transmitting large amounts of power from a central position to several separate stations; there is little energy lost in the transmission of this power; control is positive in nature; and it is possible to sustain forces without expending further energy. Furthermore, large power amplifications are possible; it is also possible to govern a considerable amount of horsepower with a few watts of control. Hydraulic controls can easily be tied into electrical networks and can be designed to perform almost any kind of work.
At the present time, there are four reasons why hydraulics is not used in certain types of guided missiles:
(1) Lack of small, efficient power reservoirs or generators
(2) Unreliable operation at climatic extremes
(3) Tendency of hydraulic systems to leak, and
( 4) Storage problems.
Considerable research and development is being conducted in the hydraulics field in an attempt to create small, efficient hydraulic reservoirs of power to compete with batteries and to eliminate the sticking and freezing of control valves and other components at climatic extremes. Under the latter conditions, failures do not often occur from a fault or failure of the oil itself, but rather from the "freezing" of moving parts which operate under close tolerances.
Hydraulics has an excellent opportunity of becoming the leading workhorse for modern guided missile control systems.