Digital resolution and other digital subjects, part 1
Editor's note: This is the first installment in a seven-part series on digital resolution and other subjects. Read the rest now: Part 2, Part 3, Part 4, Part 5, Part 6, and Part 7.
The increasing use of digital technology in our daily lives, and the ability of programmers to hide the technology taking place underneath, can leave even the most technically minded confused. For example, when I boot my computer with Windows, open WordPerfect to compose a document, then click on the Print icon, who is responsible for the arcane display of printing options that confront me before I get to see my printout? It looks much like the window that appears when I click to print a Portable Document Format (PDF) file from Adobe Reader or from Microsoft’s own NotePad.
As long as everything works, and if I can figure out how to select the options, I’ll see pages coming out of the printer. But if that doesn’t happen, who do I call on to fix the problem? Is it a WordPerfect problem, a Hewlett-Packard problem, or, heaven forbid, a problem with Windows? Confusion is the legacy of an industry-wide effort, started a couple of decades ago, to develop human machine interfaces (HMIs) that are “seamless.”
Seamless, or obscure?
Seamlessness is that property given to a series of interacting computer programs that obscure who is responsible and where the program is actually running. At any given moment, it may be running on your computer, or maybe somewhere in cyberspace. It’s difficult to tell, and equally difficult to allocate responsibility.
I can’t promise to dissolve the barriers of seamlessness, but I can talk about some of the basics of digital systems. Therefore, if confronted with modern digital control systems for electrohydraulic machinery, you should have a better chance of successfully dealing with the day-to-day challenges. It all begins with the lowly zeroes and ones of binary logic and the bits and bytes that ensue. A bit (no pun intended) of background might help you over some digital humps.
The heart of digital systems is a series of on-off, or binary, switches that are assembled in quantities that mimic the national debt. Overlaying that overpopulated layer of switches (actually, they are solid-state transistors, so they have no moving parts, but we still call them switches) is the fact that any decimal quantity can be represented as a series of on-off switch settings.
Bits, bytes, and binary delights
The binary numerical system is used for digital technology. Binary means that each fundamental element has two states: On (1) or off (0). Most light switches are binary devices, because they can be either on or off. Transistors can be configured in circuits so that they are either on or off, so each transistor is a binary device. They are referred to as switches, but they are not mechanical in the same sense that the light switch is. They are switches because they are binary.
A modern microprocessor chip has tens of millions of transistors, but the speeds at which they can be switched leaves us with the illusion that they are all changing instantaneously. They aren’t, they’re just very fast, with a switching time of perhaps a nanosecond. A nanosecond is one billionth of a second. To appreciate the magnitude of one billion, it would require 31.7 years to count off one billion seconds.
Transistors also have the advantage of being switched by an incoming signal voltage. This means the output of one transistor can be directed to cause another to switch, and they can be easily organized in endless arrays in combinations, called gates, which can make logical decisions. But this is getting ahead of the discussion.
Binary building blocks
Our first topic of interest is the number of combinations in which an array of switches can exist at any moment in time. One binary switch constitutes one bit. I once heard that the term bit is a sort of contraction of Binary InTeger. Each bit can have only two different values, either 0 (off) or 1 (on).
If we have two switches, they can exist in any one of four combinations — both off, the first on and the second off, the first off and the second on, or both on. Three bits produce eight unique combinations, and four bits produce 16 unique combinations. That is, if we have a circuit, or switch array consisting of N bits, then those N switches can exist in 2N different ways.
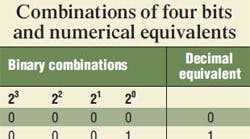
Table 1 — The total number of combinations in which N binary switches (bits) can exist is 2N. So four bits have 16 unique ways in which they can be turned on (1) or off (0).
Table 1 shows the combinations for a 4-bit array. The first four columns are a tabulation of all 16 combinations in which the four switches can exist, and the fifth column is the decimal equivalent of each row.
Each row in the table has a unique combination of ones and zeros. The first row has the binary number of 000 and represents the decimal value of 0, which should not be surprising. The binary number 0111 can be thought of as (0 × 8) + (1 × 4) + (1 × 2) + (1 × 1), which is, of course, seven.
It’s easy to convert binary numbers to their decimal equivalent values by simply using the powers of 2 at the tops of each binary column. That is, the binary number 0101 is evaluated as:
0101 = 0 × 23 + 0 × 22 + 0 × 21 + 0 × 20= 5.
This can also be written as:
01012 = 510,
where 0101 is in binary (base 2), the same as five in base 10, which is our common decimal notation.
It is also easy to go the other way, that is, convert decimal to binary, but it isn’t necessary, and it would only detract from the real aim, which is to address some of the basic digital issues that confront practitioners of the electrohydraulics without becoming experts in binary math.
The important issue is that Table 1 shows 16 different binary combinations, the first decimal value for which is 0 and the last is 15, not 16. This leads us to two of the most important realities of binary notation:
2N is the total number of combinations, and the maximum value is 2N – 1.
So if we have four bits, the total number of combinations is 16, and biggest quantity that can be indicated is one less than that, or 15. If we have 10 bits, the total number of combinations is 210, which is 1024. If we have 20 bits, the number of combinations is 1,048,576, and the biggest number that can be stored (as in a 20-bit memory location) is 1,048,575.
Order forms patterns
Refer again to Table 1 and look at the fourth column, the one headed by 20. Look at the 1 and 0 pattern. It is a zero followed by a one. The next column, the 20 column, has two zeros followed by two ones, and the next column to the left is four zeros followed by four ones, and so on, until the total number of combinations is reached. When constructed in this manner, the table of binary values increases by one from row to row, and no two rows have the same pattern.
Thus, we reach another important conclusion: Any quantity can be represented as an equivalent binary number. Good thing, too, because all our computers work in binary, but they have to calculate our paychecks in decimal format. If they didn’t, a check for $500 would instead be 111110100. It should be apparent, then, that listing all combinations for a certain number of bits would require quite a large table. Fortunately, we rarely have to do that.
The byte is a fabricated term to aid the creation of a so-called “computer word.” The term byte was coined in the earliest days of the digital revolution by Dr. Werner Buchholz, of IBM, in July 1956. Byte became the basic unit for microprocessors in the 1970s. That is, the basic computer “word length” was chosen to be eight bits (one byte), but it is a de facto standard. But not all computers have 8-bit word lengths, so “bytes” can have differing numbers of bits depending on the application. However, bytes commonly applied in the industrial world have eight bits, so we will adopt that convention for this discussion.
The ASCII (American Standard Code for Information Interchange) codes occupy 7 bits, meaning that 128 different characters (including 0) can be represented. That’s enough combinations to include all letters of the alphabet in both upper and lower case, the ten integers in our counting system, common punctuation symbols, and a few extras.
Microsoft, in some of its user manuals, unabashedly lists 8 bits worth of ASCII characters, which has 256 combinations and host of additional characters. Some call this an extended ASCII character set. The common lexicon is not standardized. What is interesting though, is that the computer industry, in defining the basic word length, ended up with a word length that can accommodate only a single character. Such is the stuff of which confusion is made.
Those old enough may recall that the first practical microprocessors used 8-bit bytes. Then came the 16-bit and the 32-bit, and now 64 bit microprocessors are available. But the byte remains the basic unit. These microprocessors were built with 1-, 2-, 4-, and 8-byte integrated circuit chips. Digital components are expressed in both bits and bytes.
The hard drive on your computer tends to be rated in GB, meaning gigabytes (billions of bytes), and now, even TB, meaning terabytes (trillions of bytes). The use of capital B in MB and TB is deliberate. It indicates bytes. On the other hand, your high speed internet connection is most likely rated in Mb/sec, meaning millions of bits/sec, because of the lower case b. Just remember there are eight bits in every byte. The byte takes a bigger bite of the binary world than does the itty-bitty bit.